Dalam teori komputabilitas dan teori kompleksitas komputasi , pengurangan adalah transformasi dari satu masalah ke masalah lain.Tergantung pada transformasi yang digunakan ini dapat digunakan untuk mendefinisikan kelas kompleksitas pada serangkaian masalah.
Secara intuitif, masalah A ke B direduksi masalah jika solusi ke B ada dan memberikan solusi ke A setiap kali A memiliki solusi. Jadi, pemecahan A tidak bisa lebih sulit daripada memecahkan B. Kita menulis A ≤ m B, biasanya dengan subskrip pada ≤ untuk menunjukkan jenis pengurangan yang digunakan (m: pengurangan pemetaan, p: reduksi polinomial).
Sering kali kita menemukan diri kita berusaha untuk memecahkan masalah yang mirip dengan masalah kita sudah dipecahkan. Dalam kasus ini, sering merupakan cara cepat untuk memecahkan masalah baru untuk mengubah setiap contoh dari masalah baru ke contoh dari masalah lama, memecahkan ini menggunakan solusi yang ada, dan kemudian menggunakan ini untuk mendapatkan solusi akhir kami. Ini mungkin adalah penggunaan paling jelas dari pengurangan.
Penggunaan lain, lebih halus adalah ini: misalkan kita punya masalah yang kami telah terbukti sulit untuk memecahkan, dan kami memiliki masalah baru yang sama. Kita mungkin menduga bahwa hal ini juga, sulit untuk memecahkan. Kami berpendapat dengan kontradiksi: rasa masalah baru mudah untuk memecahkan. Kemudian, jika kita dapat menunjukkan bahwa setiap instance dari masalah lama dapat diselesaikan dengan mudah dengan mengubahnya menjadi contoh dari masalah baru dan memecahkan mereka, kami memiliki kontradiksi. Ini menetapkan bahwa masalah baru juga keras.
Sebuah contoh yang sangat sederhana dari pengurangan adalah dari perkalian untuk mengkuadratkan. Misalkan semua kita tahu bagaimana melakukannya adalah untuk menambah, mengurangi, mengambil kotak, dan dibagi dengan dua. Kita dapat menggunakan pengetahuan ini dikombinasikan dengan rumus berikut, untuk memperoleh produk dari dua angka:
Kami juga memiliki penurunan arah lain, jelas, jika kita dapat mengalikan dua angka, kita bisa persegi nomor. Hal ini tampaknya menyiratkan bahwa dua masalah sama-sama keras. Semacam ini pengurangan sesuai dengan pengurangan Turing .
Namun, pengurangan menjadi jauh lebih sulit jika kita menambahkan pembatasan bahwa kita hanya dapat menggunakan fungsi mengkuadratkan satu kali, dan hanya di akhir. Dalam hal ini, bahkan jika kami diizinkan untuk menggunakan semua operasi aritmatika dasar, termasuk perkalian, pengurangan tidak ada pada umumnya, karena kita mungkin harus menghitung suatu bilangan irasionalseperti  dari nomor rasional. Pergi ke arah lain, bagaimanapun, kita pasti bisa persegi nomor hanya dengan satu perkalian, hanya di akhir. Menggunakan bentuk terbatas pengurangan, kami telah menunjukkan hasil mengejutkan bahwa perkalian lebih sulit secara umum dari mengkuadratkan. Hal ini sesuai dengan banyak-satu pengurangan .
dari nomor rasional. Pergi ke arah lain, bagaimanapun, kita pasti bisa persegi nomor hanya dengan satu perkalian, hanya di akhir. Menggunakan bentuk terbatas pengurangan, kami telah menunjukkan hasil mengejutkan bahwa perkalian lebih sulit secara umum dari mengkuadratkan. Hal ini sesuai dengan banyak-satu pengurangan .
 dari nomor rasional. Pergi ke arah lain, bagaimanapun, kita pasti bisa persegi nomor hanya dengan satu perkalian, hanya di akhir. Menggunakan bentuk terbatas pengurangan, kami telah menunjukkan hasil mengejutkan bahwa perkalian lebih sulit secara umum dari mengkuadratkan. Hal ini sesuai dengan banyak-satu pengurangan .
dari nomor rasional. Pergi ke arah lain, bagaimanapun, kita pasti bisa persegi nomor hanya dengan satu perkalian, hanya di akhir. Menggunakan bentuk terbatas pengurangan, kami telah menunjukkan hasil mengejutkan bahwa perkalian lebih sulit secara umum dari mengkuadratkan. Hal ini sesuai dengan banyak-satu pengurangan .Diberikan dua himpunan bagian A dan B dari N dan satu set fungsi F dari N ke N yang tertutup di bawah komposisi , A disebut direduksi ke B di bawah F jika
Kami menulis
Misalkan S adalah subset dari P (N) dan pengurangan ≤, maka S disebut tertutup di bawah ≤ jika
Subset A N disebut sulit bagi S jika
Subset A N disebut lengkap untuk S jika A sulit untuk S dan A adalah S.
Reduksi adalah preordering , yang merupakan refleksif dan transitif relasi , pada P (N) × P (N), di mana P (N) adalah kekuatan diatur dari alam nomor .Seperti dijelaskan dalam contoh di atas, ada dua jenis utama yang digunakan dalam pengurangan kompleksitas komputasi, banyak pengurangan-satu dan pengurangan Turing . Banyak-salah satucontoh peta pengurangan satu masalah terhadap kasus lain; turing pengurangan menghitung solusi untuk satu masalah, dengan asumsi masalah lainnya adalah mudah untuk dipecahkan. Penurunan banyak-satu adalah lebih lemah dari pengurangan Turing. Pengurangan lemah lebih efektif dalam memisahkan masalah, tetapi mereka memiliki lebih sedikit daya, membuat pengurangan sulit untuk desain.
Masalahnya adalah lengkap untuk kelas kompleksitas jika setiap masalah di kelas mengurangi masalah itu, dan juga di kelas itu sendiri. Dalam pengertian ini mewakili masalah kelas, karena setiap solusi untuk itu bisa, dalam kombinasi dengan pengurangan, digunakan untuk memecahkan setiap masalah di kelas.
Namun, untuk menjadi berguna, pengurangan harus mudah. Sebagai contoh, itu sangat mungkin untuk mengurangi sulit-untuk-mengatasi NP-lengkap masalah seperti masalah satisfiability booleanuntuk masalah sepele, seperti menentukan jika nomor sama dengan nol, dengan memiliki mesin reduksi memecahkan masalah dalam waktu eksponensial dan output nol hanya jika ada solusi.Namun, hal ini tidak mencapai banyak, karena meskipun kita dapat memecahkan masalah baru, melakukan pengurangan hanya sekeras memecahkan masalah lama. Demikian pula, penurunan komputasi fungsi noncomputable dapat mengurangi suatu masalah diputuskan untuk satu decidable. Seperti Michael Sipser menunjukkan dalam Pengantar Teori Perhitungan: "Penurunan harus mudah, relatif terhadap kompleksitas masalah-masalah khas di kelas [...] Jika pengurangan itu sendiri sulit untuk menghitung, solusi mudah untuk menyelesaikan masalah tidak akan selalu menghasilkan sebuah solusi mudah untuk mengurangi masalah untuk itu. "
Oleh karena itu, gagasan yang sesuai pengurangan tergantung pada kelas kompleksitas sedang dipelajari. Ketika mempelajari kompleksitas kelas NP dan kelas keras seperti hirarki polinomial ,polinomial-waktu pengurangan digunakan. Ketika mempelajari kelas-kelas dalam P seperti NC dan NL , log-ruang pengurangan digunakan. Penurunan juga digunakan dalam teori komputabilitas untuk menunjukkan apakah masalah atau tidak dipecahkan oleh mesin sama sekali, dalam hal ini, pengurangan dibatasi hanya untuk fungsi dihitung .
Dalam hal optimasi (memaksimalkan atau minimisasi) masalah, kita sering berpikir dalam hal pendekatan-melestarikan pengurangan. Misalkan kita memiliki masalah optimasi dua seperti bahwa kasus-kasus satu masalah dapat dipetakan ke kasus yang lain, dengan cara yang hampir-solusi yang optimal terhadap kasus masalah terakhir dapat diubah kembali untuk menghasilkan solusi optimal untuk hampir-mantan. Dengan cara ini, jika kita memiliki algoritma optimasi (atau algoritma aproksimasi ) yang menemukan dekat-optimal (atau optimal) solusi untuk contoh dari B masalah, dan pengurangan pendekatan-melestarikan efisien dari A ke B masalah masalah, dengan komposisi kita memperoleh optimasi algoritma yang menghasilkan solusi yang optimal dekat terhadap kasus masalah A. Pendekatan-melestarikan pengurangan sering digunakan untuk membuktikan kekerasan pendekatan hasil: jika beberapa masalah optimasi adalah sulit untuk perkiraan (di bawah beberapa asumsi kompleksitas) dalam faktor lebih baik dari α untuk beberapa α, dan ada β-pendekatan-melestarikan pengurangan dari masalah A B masalah untuk, kita dapat menyimpulkan bahwa B masalah adalah sulit untuk perkiraan dalam faktor α / β.
Contoh
- Untuk menunjukkan bahwa masalah keputusan P diputuskan kita harus menemukan pengurangan dari masalah keputusan yang sudah diketahui diputuskan untuk fungsi pengurangan P. Itu harus menjadi fungsi dihitung . Secara khusus, kita sering menunjukkan bahwa P Masalahnya diputuskan dengan menunjukkan bahwa masalah menghentikan mengurangi ke P.
- Kelas kompleksitas P , NP dan PSPACE yang tertutup di bawah polinomial-waktu pengurangan .
- Kelas kompleksitas L , NL , P , NP dan PSPACE yang tertutup di bawah log-ruang pengurangan .
Contoh rinci
Contoh berikut menunjukkan bagaimana menggunakan pengurangan dari masalah terputus-putus untuk membuktikan bahwa bahasa adalah diputuskan. Misalkan H (M, w) adalah masalah menentukan apakah yang diberikan mesin Turing M menghentikan (dengan menerima atau menolak) pada string input w. Bahasa ini dikenal diputuskan. Misalkan E (M) adalah masalah menentukan apakah bahasa mesin Turing diberikan M menerima kosong (dengan kata lain, apakah menerima setiap string M sama sekali). Kami menunjukkan bahwa E diputuskan oleh penurunan dari H.
Untuk mendapatkan kontradiksi, misalkan R adalah penentu untuk E. Kami akan menggunakan ini untuk menghasilkan penentu S untuk H (yang kita tahu tidak ada). Mengingat masukan M dan w(mesin Turing dan beberapa string masukan), mendefinisikan S (M, w) dengan perilaku berikut: S N Turing menciptakan mesin yang menerima hanya jika string masukan ke N adalah w dan Mperhentian pada input w , dan tidak menghentikan sebaliknya. Penentuan S sekarang dapat mengevaluasi R (N) untuk memeriksa apakah bahasa yang diterima oleh N kosong. Jika R menerima N,maka bahasa yang diterima oleh N kosong, sehingga dalam M tertentu tidak menghentikan pada input w, sehingga S dapat menolak. Jika R menolak N, maka bahasa yang diterima oleh N tidak kosong, sehingga M tidak menghentikan pada input w, sehingga S dapat menerima. Jadi, jika kita memiliki R penentu untuk E, kita akan mampu menghasilkan penentu S untuk masalah Hmenghentikan (M, w) untuk setiap M mesin dan masukan w. Karena kita tahu bahwa seperti S tidak dapat ada, maka bahasa bahwa E juga diputuskan.



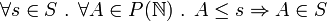

Tidak ada komentar:
Posting Komentar